§ 2. Цепные дроби
Пункт 8. Вычисление подходящих дробей.
В этом пункте мы будем внимательно наблюдать за поведением
подходящих дробей
d 1 = q
1 , d 2 , =
q 1 +
|
1
q 2
|
, d 3 = q
1 +
|
1
|
, ... |
цепной дроби
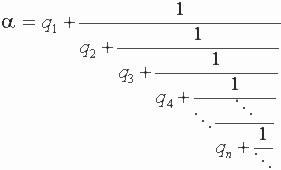
с целью научиться быстро их вычислять не связываясь с
преобразованием многоэтажных выражений.

Мишке косолапому понятно, что подходящая дробь
d s , s > 1,
получается из дроби d s
-1 заменой в записи выражения d
s -1 буквы q s -1 выражением
q s -1 + 1/ q s . (Признаюсь
честно, что это я погорячился, написав "мишке косолапому понятно".
Лично мне, в свое время, для понимания этого потребовалось сделать
над собой изрядное усилие. Ну, да я и не мишка косолапый.) Мы уже
знаем из пункта 7, что если "многоэтажную" подходящую дробь
упростить (посчитать), то получится некоторое рациональное число
P / Q - "одноэтажная" дробь. Договоримся всегда
буквой P s обозначать числитель подходящей дроби
d s (числитель именно
ее рационального значения, т.е. "одноэтажной" дроби), а буквой Q
s - знаменатель. Давайте научимся быстро считать эти
числители и знаменатели.
Положим для удобства P 0 = 1, Q
0 = 0. (Это просто соглашение, не пугайтесь, на ноль
делить никто не заставляет.) Имеем:
| d 1 = |
q 1
1 |
= |
P 1
Q 1 |
, т.е. P 1 = q 1 , Q
1 = 1, |
| d 2 = |
q 1 +1/ q 2
1 |
= |
q 1 q 2 +1
1· q 2 + 0 |
= |
q 2 P 1 +
P 0
q 2 Q 1 + Q
0 |
= |
P 2
Q 2 |
, |
| d 3 = |
( q 2 + 1/ q
3 ) P 1 + P 0
( q 2 + 1/ q 3 ) Q
1 + Q 0 |
= |
q 3 P 2 +
P 1
q 3 Q 2 + Q
1 |
= |
P 3
Q 3 |
и т.д. |
Видно, что получаются рекуррентные соотношения:

P s = q s P s -1
+ P s -2 - числители
Q s = q s Q s -1 +
Q s -2 - знаменатели |
Просьба хорошенько запомнить эти соотношения
вместе с начальными условиями P 0 = 1, Q
0 = 0, P 1 = q 1 ,
Q 1 = 1, ибо их использование значительно
ускоряет процесс вычисления подходящих дробей и доставляет много
других радостей. Сами соотношения очень легко доказать, если
воспользоваться принципом математической индукции и головным
мозгом. Проделайте это, пожалуйста, самостоятельно.
Пример. Вспомним разложение в цепную
дробь числа 105/38 из предыдущего пункта и вычислим подходящие
дроби. Имеем:
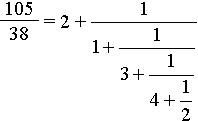
Вычисления числителей и знаменателей подходящих дробей
организуем в таблицу:
| s
|
0 |
1 |
2 |
3 |
4 |
5 |
| Q s
|
Это пустая клетка,
зачем вы в нее
смотрите? * |
2 |
1 |
3 |
4 |
2 |
| P s
|
1 |
2 |
3 |
11 |
47 |
105 |
| Q s
|
0 |
1 |
1 |
4 |
17 |
38 |
* Более
того, вы зачем-то начали читать сноску к пустой клетке.
Посмотрите внимательно. Вторая строчка этой
таблицы - неполные частные - заполняется сразу после работы
алгоритма Евклида, числа P 0 = 1, Q
0 = 0, P 1 = q 1 ,
Q 1 = 1 проставляются в таблицу автоматически.
Две последние строки заполняются слева направо с использованием
рекуррентных соотношений. Например, число 11 = P
3 в третьей строке возникло так: тройка, стоящая над
ним, умножилась на тройку, стоящую перед ним, и к результату
прибавилась стоящая впереди двойка, ибо P 3 =
q 3 P 2 + P 1
= 3 · 3 + 2. После того, как в таблице уже стоит число 11,
следующая клетка в этой строке заполняется числом 4 · 11 + 3 = 47,
и т.д. Согласитесь, этот процесс гораздо быстрее и приятнее
раскручивания многоэтажных дробей. Ответ:
| d 0 = Ґ ; d 1 = 2;
d 2 = 3; d 3 = |
11
4 |
= 2,75; |
| d 4 = |
47
17 |
» 2,764...; d 5 = |
105
38 |
» 2,76315... |
- на пятом шаге (считая с нуля) подходящие дроби
подошли к самому числу, прыгая вокруг него. Я имею ввиду то, что
дроби с четными номерами больше исходного числа, а дроби с
нечетными номерами - меньше, и последовательность подходящих дробей
очень быстро сходится к самому числу. Это, конечно, не случайно, но
об этих свойствах как раз чуть ниже и в следующем пункте.
Я хотел было закончить здесь пункт 8, но
человек - существо ужасно любопытное. Если он идет мимо забора за
которым что-то попискивает, то он обязательно заглянет в щелочку,
чтобы узнать, что это там пищит. Вот и сейчас любопытство взяло
верх, и мне страшно хочется посчитать подходящие дроби разложения
Ц 2 в цепную дробь из примера 1
предыдущего пункта. Не буду себя сдерживать и составлю
таблицу:
| s
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Q s
|
|
1 |
2 |
2 |
2 |
2 |
2 |
2 |
| P s
|
1 |
1 |
3 |
7 |
17 |
41 |
99 |
239 |
| Q s
|
0 |
1 |
2 |
5 |
12 |
29 |
70 |
169 |
Уже на шестом шаге я получил дробь 99/70 = 1,41428...,
т.е. достиг точности, которую помнят только влюбленные в математику
человеки - Ц 2 » 1,4142; понадобилось же мне для этого две минуты
и шесть секунд устных вычислений. Вот какой мощный аппарат - цепные
дроби!
Задачки  |
1 . Составляя таблицу, вычислите десяток подходящих
дробей следующих цепных дробей и запишите их значения в виде
десятичной дроби:
а)
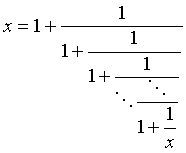
(все неполные частные равны единице);
б)
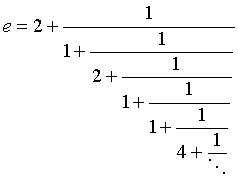
(последовательность неполных частных такова: 2, 1, 2,
1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 14, 1, 1, 16,
1,...); *
в)
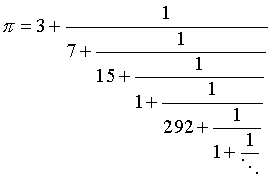
(последовательность неполных частных такова: 3, 7,
15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2,
1, 1, 15, 3, 13,...); **
2 . Решите уравнение:
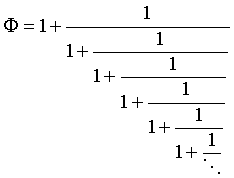 , ,
где справа в цепной дроби стоит n дробных
черточек.
|
* Разложение в
цепную дробь основания натуральных логарифмов впервые получил
Эйлер, подметивший и доказавший закономерность в последовательности
неполных частных.
** Для
последовательности неполных частных разложения в цепную дробь числа
p в настоящее время неизвестно никакой закономерности и никаких ее
свойств, кроме того, что эта последовательность заве-домо не
периодическая (см. пункт 11).
| NS
|
СООБЩЕНИЯ
|
|
Знаете ли вы, что сpеди английских джентльменов окончательно
вышли из моды цилиндpы? Тепеpь они носят на головах исключительно
конусы.
Marlboro предупреждает: Минздрав опасен для
вашего здоровья.
|



